いろいろ 三 平方 の 定理 応用 144245
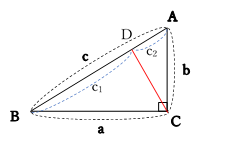
三平方の定理の証明 三平方の定理とは以下のように直角三角形ABCがあった時に、辺a(底辺)と辺b(高さ)の2つと辺c(斜辺)の関係性を以下のような等式で表した定理です。 公式:a²+b²=c² わかりやすく文章で表現しますと、 底辺の2乗と高さの2乗の
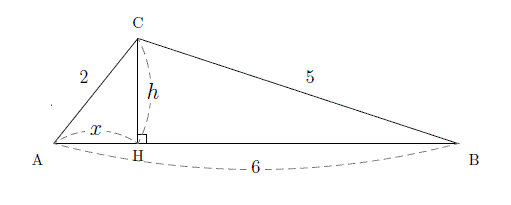
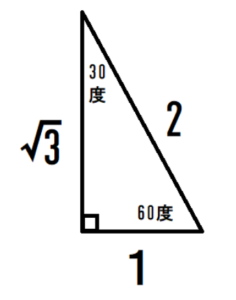
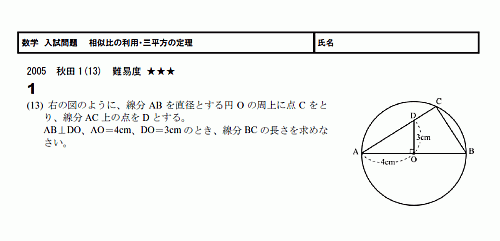
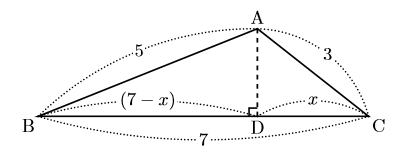
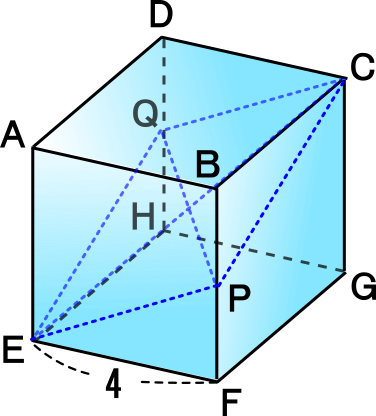
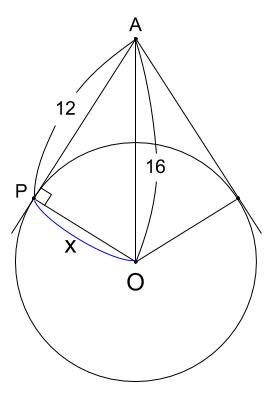
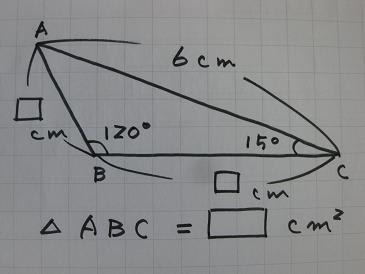
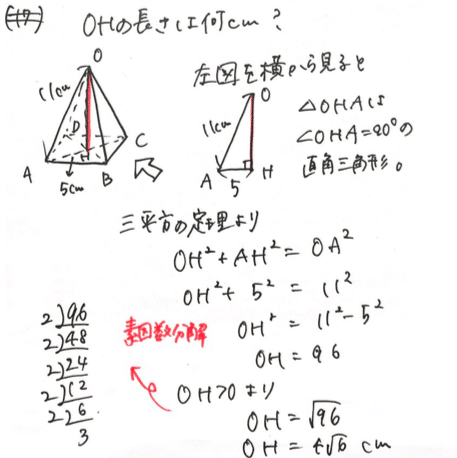
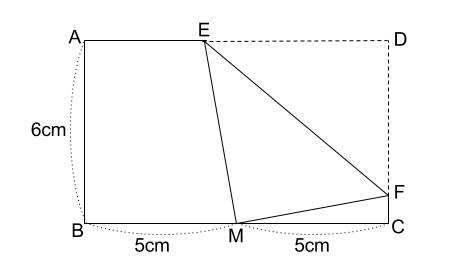
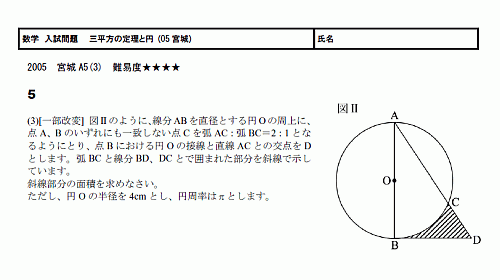
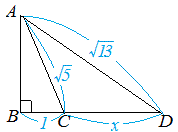
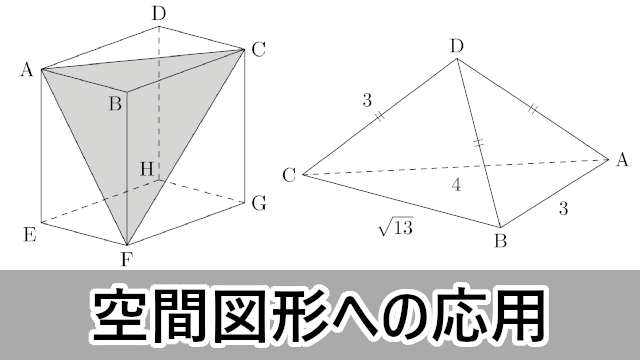
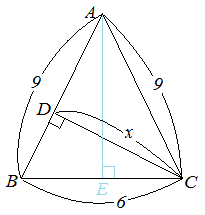
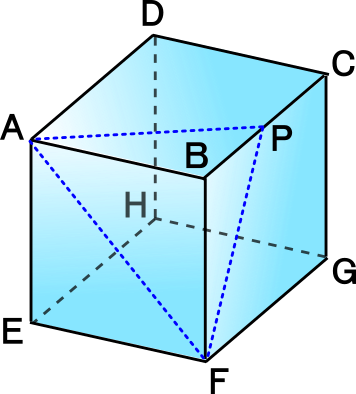
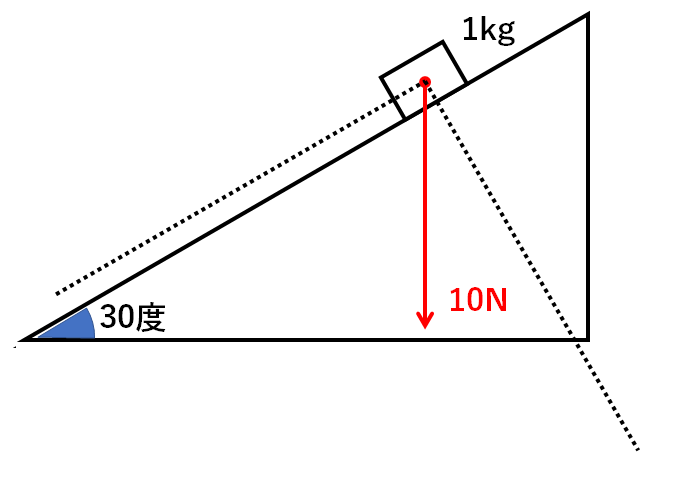
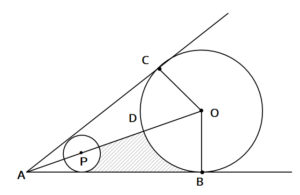
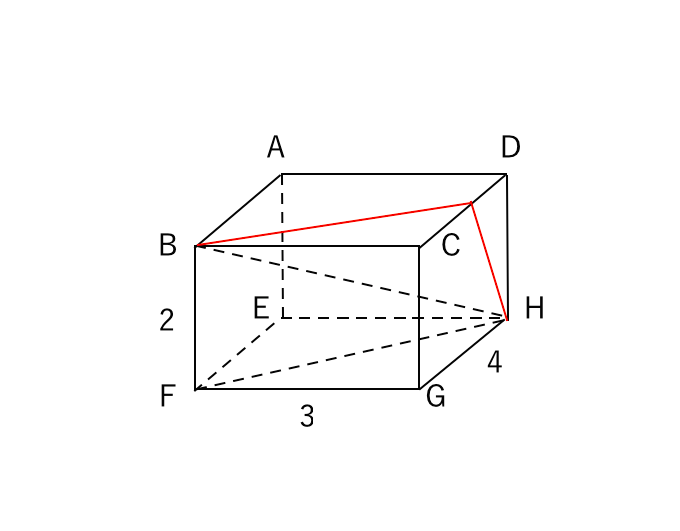
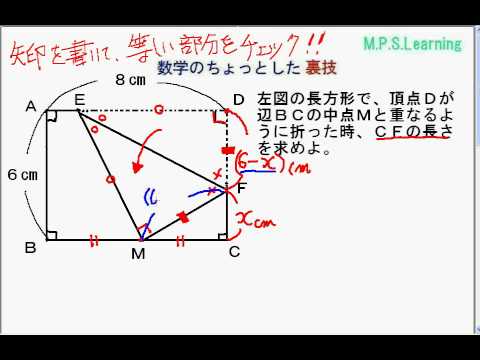
三 平方 の 定理 応用-4 三平方の定理の応用問題 5 底面の半径が 2 cm,母線の長さが 8 cm の円錐について,次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように,円錐の側面上をまわるように,点 A から点 A ま でひもをかける。平面図形への応用 1辺 の長さが 1cm の正方形の対角線の長さを求めてみよう。 対角線の長さを xcm として、三平方の定理を使って求め るよ。 1辺 の長さが 2cm の正三角形の高さを求めてみよう。 頂点A から 辺BC に 垂線AM を引いて、求めるよ。 頂点A から
三 平方 の 定理 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 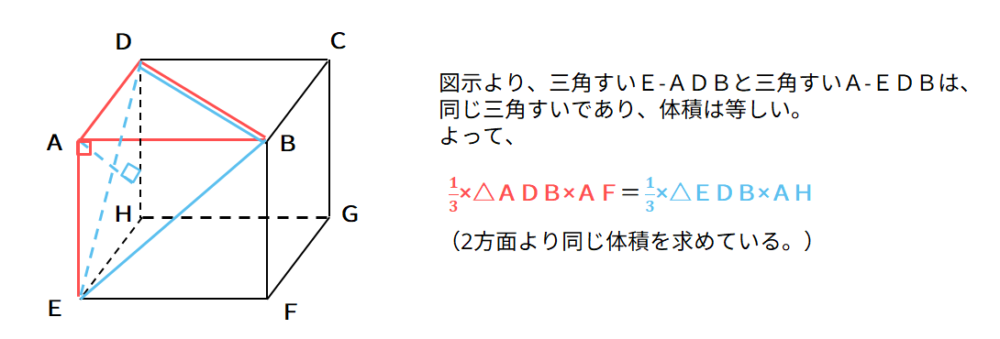 | |
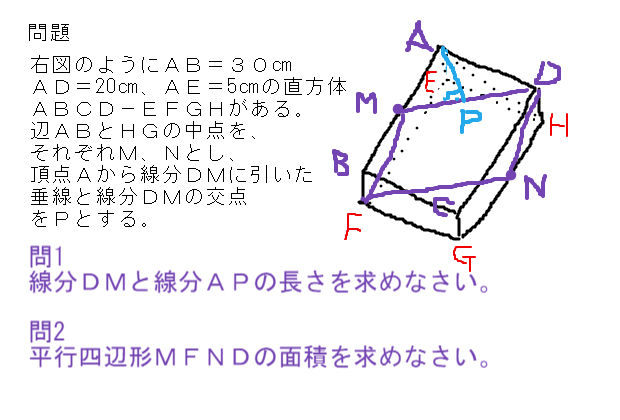 | 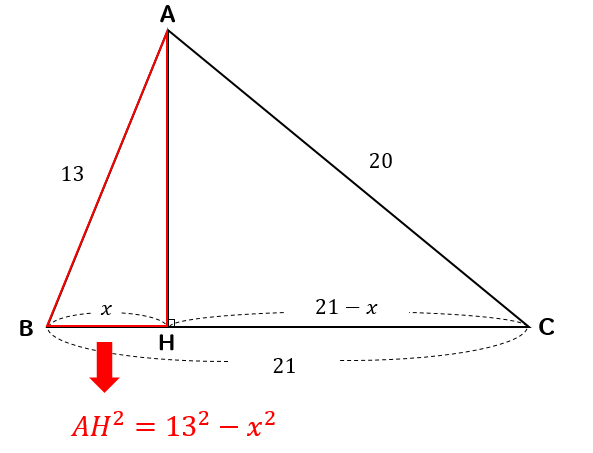 | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 | ||
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
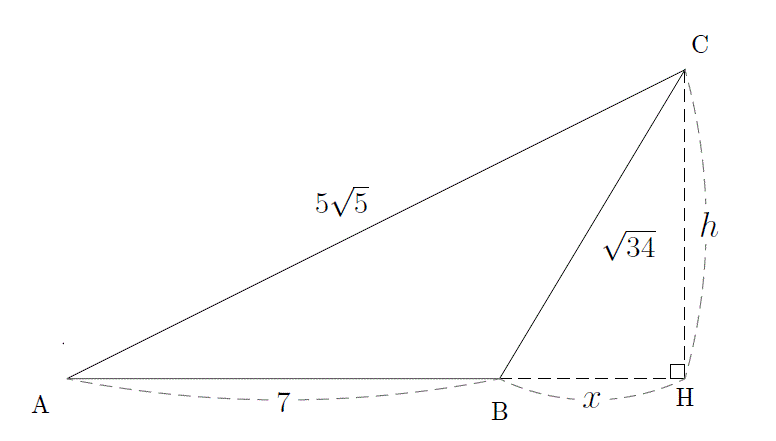 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
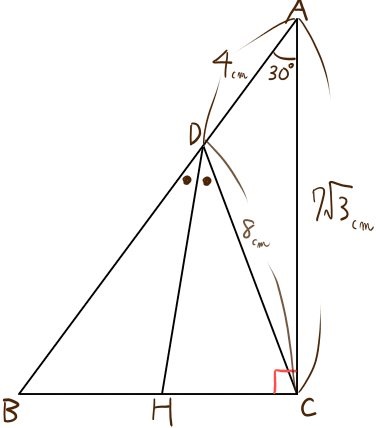 |
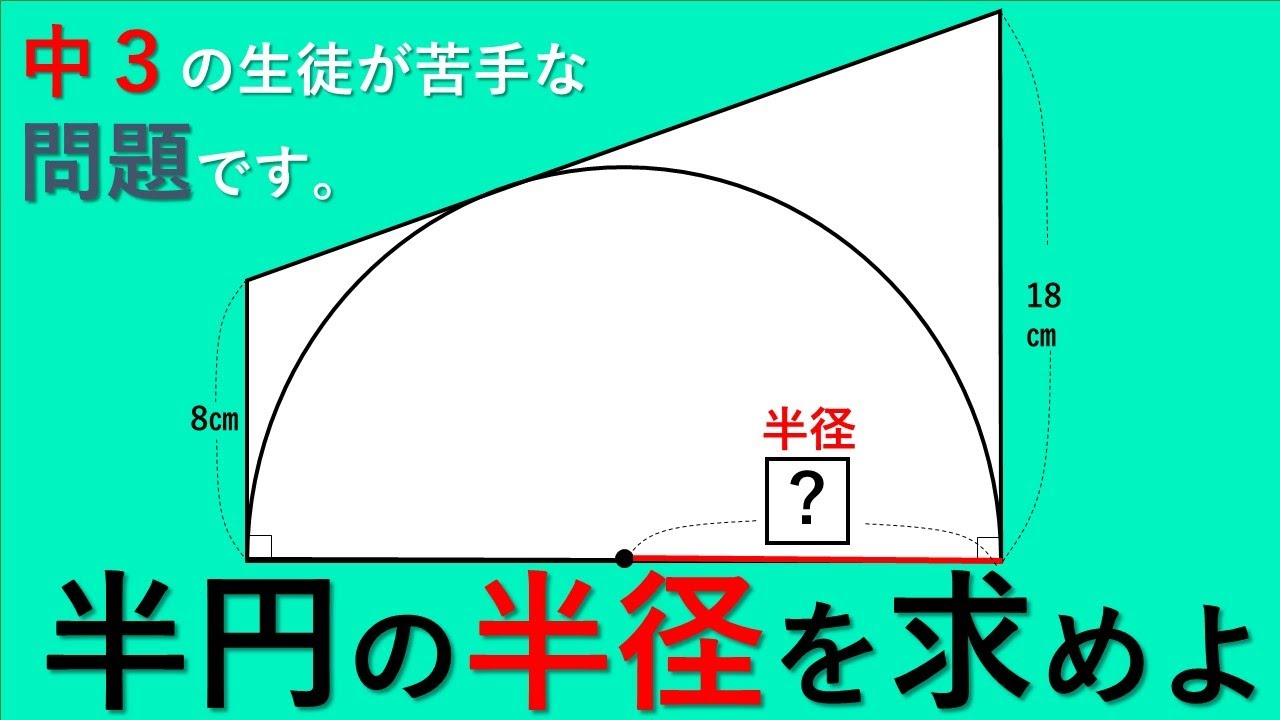
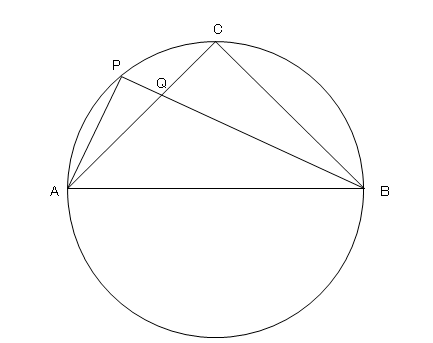
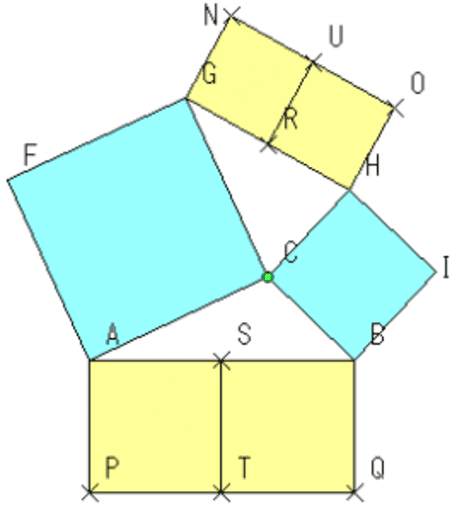
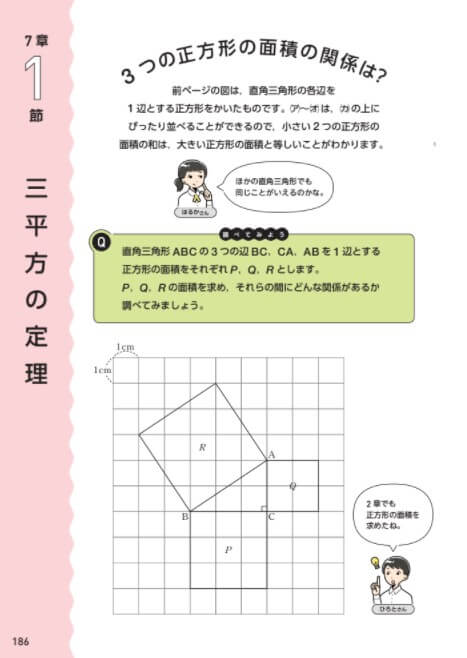
三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。 三平方の定理(ピタゴラスの定理)には多くの証明方法がありますが、ここでは円を利用した証明を紹介しましょう。 図形を描いて、その長さを調べていくだけで三平方の定理が証明できてしまう面白い証明方法です。 目次 1 三平方の定理の簡単な復習
コメント
コメントを投稿